Monthly Archives: February 2018

Recovery, Rocket Building

Creating sleeves for the Shock-Cord

I wanted to protect the shock-cords from the brutal heat of the ejection charge. I knew I can purchase nomex variants, but I didn’t have any place I could purchase them easily and I thought I’d try my chances and make something that might provide them “some” protection at minimal cost.

The solution needs to provide some protection for a few flights. It doesn’t need to be so strong it will last 20 flights. i.e. something modest is satisfactory.

Materials

I did some research on materials and it seems that:-

  • Wool is not flammable
  • Cotton is probably not too bad a material at resisting fire.
  • There are some Polyesters that are impregnated with some compounds that make them inflammable.

I ended up finding a material that is a blend of Wool and Polyester – not perfect, but something that could provide some protection over 2 or 3 flights before requiring replacement.

Creating the sleeve

It was quite a simple process, however I thought it would be important to show some photos below of what I did.

 

Fabric is roughly cut out.
Fabric is roughly cut out.
Pinned the fabric length wise.
Pinned the fabric length wise.
Comparing pinned fabric with shock-cord to make sure the shock-cord will fit inside it.
Comparing pinned fabric with shock-cord to make sure the shock-cord will fit inside it.
Sewing the sleeve with my sewing machine, using the pins as a guide and removing them as I approach them.
Sewing the sleeve with my sewing machine, using the pins as a guide and removing them as I approach them.
Finished sewing sleeve.
Finished sewing sleeve.
Trimmed the sewn sleeve - make it look neat.
Trimmed the sewn sleeve – make it look neat.
Shock-cord in sleeve.
Shock-cord in sleeve.
Shock-Cord bowline knot around the Quicklink.
Shock-Cord bowline knot around the Quicklink.
Sleeve fits snugly around the whole bowline knot. Later on, I use zip-ties to hold it in place and reduce chance of hot gases going up length of sleeve.
Sleeve fits snugly around the whole bowline knot. Later on, I use zip-ties to hold it in place and reduce chance of hot gases going up length of sleeve.

How does it fair?

The result of two ejection tests. This sleeve needs to be replaced.
The result of two ejection tests. This sleeve needs to be replaced.

 

Cut open of sleeve shows interior is fairly untouched. The Shock-Cord looks like it is relatively good health
Cut open of sleeve shows interior is fairly untouched. The Shock-Cord looks like it is relatively good health
L2 Certification, Rocket Building

Parachute Sizing + Shock Cord

Drogue Parachute

Very particular about having a Drogue parachute used at the top of the flight. They are supposed to be built to survive extra forces. The choice of Drogue parachute is important because when the main parachute is ejected, I don’t want the rocket travelling too quickly. Some websites have said 50 to 60 mph (which translates to 22.3 ms-1 to 26.8ms-1. Open Rocket raises alerts when I hit about 22ms-1. I’d prefer to keep it within range that doesn’t produce warnings inside Open Rocket. This meant a Drogue at very minimum = 28″. Probably can’t get a 28″, so would be a 30″ Drogue.

Cert-3 Drogue Chute

I have since this found a parachute called SkyAngle CERT-3 Drogue. The main website is:-

http://www.b2rocketry.com/Cert-3.htm

The Drogue Parachute has a Cd of 1.16, but this is based on just the area of the ‘cap’, not the whole parachute. (This is not how parachutes are normally done; people usually use the whole canopy area. The website has a link to a calculator to get decent speeds:-

https://descentratecalculator.onlinetesting.net/

I put in weight of rocket as 8 kg – this is for my L2 flight. I selected the 24″ Cert-3 Drogue. Results are:-

Descent rate:

  • 70.26 ft/sec
  • 21.41 meters/sec
  • 77.09 km/hr
  • 47.9 mph

This is good. It indicates that the speed is less than 50 miles per hour.

For larger 75mm motor, L1395-BS-0, we are looking at a total weight of approximately 10.7kg. When I put these numbers into the decentrateCalculator, I get:-

Descent rate:

  • 81.26 ft/sec
  • 24.76 meters/sec
  • 89.16 km/hr
  • 55.4 mph

So this might be okay too.

How does this fair with calculations?

I would like to see if I can get similar results using well known equations.

Velocity = SQRT(8 * m * g/(pi * p * Cd * D * D))

m = 8

g = 9.81

pi = 3.1415

p = 1.22 kg/m^3

Cd = 1.16

D = 0.61cm (24″)

Putting this all in, we get:-

V = 19.5ms-1.

This does not agree with above calculated values. It is slightly under.

What are the Risks with a 24″ Drogue Chute?

The main concern is that the speed of the rocket is such that as the main parachute is ejected, it shreds it, or it damages the rocket in another way, e.g. rips out the shock-cord.

It is probably helpful to also list what we consider to not be a risk

  • Shredding of the Drogue

We can probably do a small calculation to determine the approximate forces that the rocket will experience due to the deployment of the main parachute.

F = ma

m = 8kg

a = Delta V/ Delta T

Delta V = 6 – 22 = -16ms-1

Delta T = 0.25 seconds (BIG GUESS)

We assume the acceleration is constant

a = -16 / 0.25 = 72 ms-1

F = 8 * 64 = 516 N

64kg force = 141 lb

According to :-

https://publicmissiles.com/PMLRecoveryComponentsFAQ.pdf

The shround lines for parachutes > 48″ can take 300lbs of force.

60″ Chutes are even stronger, though there is no figures quoted.

With this in mind, even if a chute opens in 0.25 second, we are looking at a force that is probably survivable.

Main Parachute

Lots of websites suggests a landing speed of about 5 ms-1. I’m probably not going to get that, but I’m thinking I’ll get close using a 84″ PML parachute. 84″ is ~215 cm diameter. Open Rocket simulations produce a landing speed of ~5.9ms-1. I’m going to have to accept this.

Eventually I decided to go for a Cert-3 SkyAngle Large parachute. This was something Blake from AusRocketry was suggesting. I was very glad in the end to get a Cert-3 SkyAngle parachute because it is 61″ across, compared to the 84″ across….this means it is easier to pack into the airframe payload compartment. I believe me, space is a premium in that compartment.

How does this fair with calculations?

I would like to see if I can get similar results using well known equations.

Velocity = SQRT(8 * m * g/(pi * p * Cd * D * D))

m = 7.8

g = 9.81

pi = 3.1415

p = 1.22 kg/m^3

Cd = 1.26   (From the B2rocketry website)

D = 1.55m (61″)

Putting this all in, we get:-

7.3ms-1

This seems high, but if I use:-

https://descentratecalculator.onlinetesting.net/

Mass: 7.8kg

Parachute: SkyAngle Cert-3 Large

I get:-

  • 17.53 ft/sec
  • 5.34 meters/sec
  • 19.23 km/hr
  • 11.95 mph

I trust the decent calculations more than my own calculations. I suspect my D dimensions were incorrect.

Will the Cert-3 Large parachute survive or will it shred?

Now I’m obviously concerned that the 22ms-1 speed of the rocket might be too much for the main parachute. Above 20ms-1, Open Rocket shows warnings. I can see other people in posts, e.g.

http://www.rocketryforum.com/showthread.php?28347-Maximum-Parachute-Deployment-Speed

say that they have done drogueless at 24ms-1 suggesting that upper limit is 30ms-1.

Other Concern

If the Main parachute takes 5 seconds to deploy (and this is all quite possible), then at a speed of 22ms-1, the rocket will have potentially travelled 110metres (360 feet). So if I set the rocket to deploy at ~700 feet, will still have another ~110 meters to go. I think this is satisfactory.

I am contemplating changing the deploy to 1000feet. It will give it a bit more time to open.

Shock Cord

Many people suggest Tubular Nylon. It is extremely strong. AusRocketry says 9/16 version of this machines has a max tensile strength of 2000lb (that is lb, not lbf). Another site with same size material has a strength of 1500 lb. So not sure why there is a discrepancy, but perhaps I should question the AusRocketry value.

Now, let’s consider the situation where we have some Black Powder ignite and produce a pressurized chamber. Energy is neither destroyed or created, so we need to account for it. Energy would go into:-

  • Breaking the shear pins
  • Heating/moving air as its bursts the components apart
  • Imparting energy into nose cone
  • Imparting energy into the Avionics Payload

We would expect the Nose Cone and Avonics may to be sent in opposite directions (conversation of momentum) and the Shock-cord to be stretched to its maximum length and then it would produce an equal and opposite force, that keeps the components tethered. This Shockcord is effectively like a spring – and like a spring it stretches and absorbs energy. We can work out what forces are in the ShockCord based on the energy it absorbs.

F = \sqrt {2kE}.

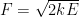k = Spring Constant

E = total energy

F = force that the Shock-Cord is experiencing.

If the force (F) is excessively large (exceeds the rated strength of the Shock-Cord), then we have  a problem.

So how much Energy is being absorbed?

The Black Powder produces a pressure and we know the volume of the tube. We assume that the Blackpowder ignites completely and the production of all these gases occur before any venting can occur. All ideal (and unlikely in the real world) but this gives us a conservative look at it.

Now, E = PV = nRT

P = 10psi = 10/14.7* 101325 ~ 69,000 Pa

V = 0.049 * 0.049 * 3.1415 * 0.41 = 0.0031m^3

E = 69,000 x 0.0031 = 213 Joules

This is a fair amount of energy.

If k = 30,000 (and this is a BIG GUESS)

F = sqrt (2 * 30,000 * 213) ~ 3600 N = 367 kg = 807 pounds

This is well short of 1500 lb or 2000 lb (AusRocketry).

Of course this all hinges on choice of k and I’m not sure if this is a good value.